返回首页 返回专题

【NOI2005】月下柠檬树 题解

这题考什么呢？当然是考我们的YY能力

首先，我们YY一下，一个水平放置的圆，经过投影到了地面会变成什么

椭圆？那你就想错了。可以自己画一画图，会发现，不管光线从什么角度照过来，它投影到地面上都还是一个完整的、与原图形一模一样的圆

那么圆锥投影到地上是什么呢？

容易想到，是一个圆、以及某点到圆的两条切线围成的图形

那么圆台呢？

YY一下发现是两个圆、以及它们的两条公切线围成的图形

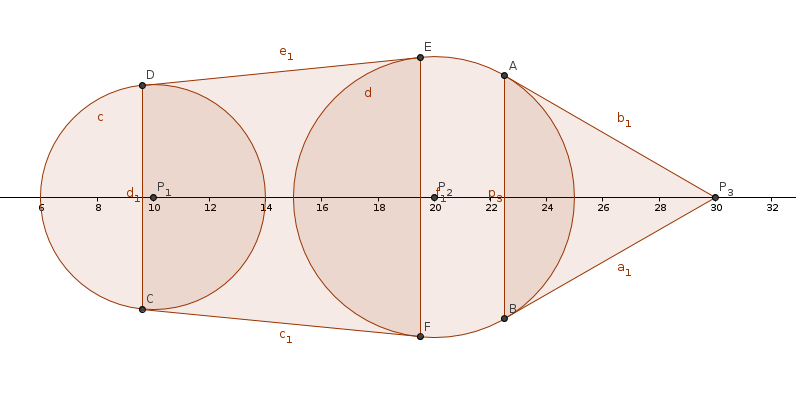
那么它的整个投影就明确了，样例的投影大致就长这样（盗的别人的图）：

投影中的圆，与原来的圆是全等的，但是两个圆之间的距离，就要根据给定的角度进行一定的伸缩，至于怎么伸缩，参考初中学的“如何计算阳光下的竖直杆影长”

#include<bits/stdc++.h>
using namespace std;

const double eps=1e-8;
struct Circle{double x,r;} c[510];
struct Trapezoid{double xl,yl,xr,yr;} ta[510];
int n=0,cnt=0;

double F(double x)
{
	int tot=0,j;double res=0;
	for(int i=1;i<=n;i++)
	{
		double tx=c[i].x-x;
		if(tx>c[i].r) continue;
		double len=sqrt(c[i].r*c[i].r-tx*tx);
		res=max(res,2*len);
	}
	for(int i=1;i<=cnt;i++)
	{
		if(ta[i].xl>x||ta[i].xr<x) continue;
		double yy=ta[i].yr-ta[i].yl;
		double xx=ta[i].xr-ta[i].xl;
		double tx=x-ta[i].xl,k=yy/xx;
		double y2=ta[i].yl+k*tx;
		res=max(res,2*y2);
	}
	return res;
}

double simpson(double a,double b)
{
	double mid=(a+b)/2;
	return (F(a)+4*F(mid)+F(b))*(b-a)/6;
}

double asr(double a,double b,double A)
{
	double mid=(a+b)/2;
	double L=simpson(a,mid),R=simpson(mid,b);
	if(fabs(L+R-A)<=15*eps) return L+R-(L+R-A)/15.0;
	return asr(a,mid,L)+asr(mid,b,R);
}
double asr(double a,double b){return asr(a,b,simpson(a,b));}

int main()
{
	double alpha,k;
	scanf("%d%lf",&n,&alpha);
	c[1].x=0;scanf("%lf",&k);
	double tana=tan(alpha);
	for(int i=1;i<=n;i++)
	{
		scanf("%lf",&k);
		c[i+1].x=c[i].x+k/tana;
	}
	double ll=1e10,rr=-1e10;
	for(int i=1;i<=n;i++)
	{
		scanf("%lf",&c[i].r);
		ll=min(ll,c[i].x-c[i].r);
		rr=max(rr,c[i].x+c[i].r);
	}
	rr=max(rr,c[n+1].x);
	double len,d,beta,fg;
	Circle c1,c2;
	for(int i=1;i<=n;i++)
	{
		double len=c[i+1].x-c[i].x;
		if(c[i+1].r>c[i].r) c1=c[i],c2=c[i+1],fg=-1;
		else c1=c[i+1],c2=c[i],fg=1;
		if(len+c1.r<=c2.r) continue;
		cnt++;d=c2.r-c1.r;
		beta=d/len;
		ta[cnt].xl=c[i].x+fg*c[i].r*beta;
		ta[cnt].xr=c[i+1].x+fg*c[i+1].r*beta;
		beta=sin(acos(beta));
		ta[cnt].yl=c[i].r*beta;
		ta[cnt].yr=c[i+1].r*beta;
	}
	printf("%.2lf\n",asr(ll,rr));
	return 0;
}