返回首页 返回专题

【BZOJ3518】点组计数 题解

权限题，给一下题面：

Description

平面上摆放着一个nm的点阵（下图所示是一个34的点阵）。Curimit想知道有多少三点组(a，b，c)满足以a，b，c三点共线。这里a，b，c是不同的3个点，其顺序无关紧要。(即(a，b，c)和(b，c，a)被认为是相同的）。由于答案很大，故你只需要输出答案对1，000，000，007的余数就可以了。

Input

有且仅有一行，两个用空格隔开的整数n和m。N,M<=50000

Output

有且仅有一行，一个整数，表示三点组的数目对1，000，000，007的余数。（1，000。000。007是质数）

Sample Input

3 4

Sample Output

2 0

题解

分三个部分来计算

第一部分是横着的三个点，其答案为n*C(m,3)

第二部分是竖着的三个点，其答案为m*C(n,3)

第三部分是斜着的三个点，网上有一个绝妙的推导：

这里用到了欧拉函数的性质：

![](http://latex.codecogs.com/gif.latex?n=\sum_{d

n}\varphi&space;(d))

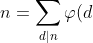简直是绝妙的一步！

#include<bits/stdc++.h>
#define Mod 1000000007
using namespace std;

typedef long long LL;
const int N=50000;
int phi[N+10];
int prime[N/5],tot=0;
bool mark[N+10];

void Init()
{
	phi[1]=1;
	for(int i=2;i<=N;i++)
	{
		if(!mark[i]) prime[++tot]=i,phi[i]=i-1;
		for(int j=1;j<=tot&&i*prime[j]<=N;j++)
		{
			mark[i*prime[j]]=1;
			if(i%prime[j]) phi[i*prime[j]]=phi[i]*(prime[j]-1);
			else{phi[i*prime[j]]=phi[i]*prime[j];break;}
		}
	}
}

int main()
{
	Init();
	int n,m;
	cin>>n>>m;
	if(n>m) swap(n,m);
	LL ans1=1ll*m*(m-1)*(m-2)/6%Mod*n%Mod;
	LL ans2=1ll*n*(n-1)*(n-2)/6%Mod*m%Mod;
	LL ans3=0;
	for(int d=1;d<n;d++)
	{
		LL res1=0;
		for(int i=1;i<=(n-1)/d;i++)
			res1=(res1+n-1ll*i*d)%Mod;
		LL res2=0;
		for(int i=1;i<=(m-1)/d;i++)
			res2=(res2+m-1ll*i*d)%Mod;
		res1=res1*res2%Mod;
		res1=1ll*phi[d]*res1%Mod;
		ans3=(ans3+res1)%Mod;
	}
	int x=0,y=0;
	for(int i=1;i<n;i++) x=(x+n-i)%Mod;
	for(int i=1;i<m;i++) y=(y+m-i)%Mod;
	ans3=(ans3-1ll*x*y%Mod+Mod)%Mod;
	ans3=ans3*2%Mod;
	LL ans=(ans1+ans2+ans3)%Mod;
	cout<<ans<<endl;
	return 0;
}